Thứ Tư, 24 tháng 7, 2019
Thứ Sáu, 14 tháng 6, 2019
Bài giảng Latex
Tài liệu ngắn gọn giới thiệu về Latex 2e
------------
Latex Beginer's Guide
----------
------------
Latex Beginer's Guide
----------
Thứ Năm, 13 tháng 6, 2019
OpenFOAM
OpenFOAM
...
History
On 8 August 2011, OpenCFD was acquired by Silicon Graphics International (SGI).[11] At the same time, the copyright of OpenFOAM was transferred to the OpenFOAM Foundation Ltd., a newly founded, not-for-profit organisation established to distribute OpenFOAM. On 12 September 2012, the ESI Group announced the acquisition of OpenCFD Ltd from SGI.[12] In 2014, Weller and Greenshields left ESI Group and continue the development and management of OpenFOAM, on behalf of the OpenFOAM Foundation, at CFD Direct.[13] CFD Direct develops OpenFOAM with a sequence based identifier (e.g. 5.0), whereas ESI-OpenCFD release OpenFOAM with a date-of-release identifier (e.g. v1806).
Distinguishing featuresSyntax One distinguishing feature of OpenFOAM is its syntax for tensor operations and partial differential equations that closely resembles the equations being solved. For example,[14] the equation
solve ( fvm::ddt(rho,U) + fvm::div(phi,U) - fvm::laplacian(mu,U) == - fvc::grad(p) );
Extensibility Users can create custom objects, such as boundary conditions or turbulence models, that will work with existing solvers without having to modify or recompile the existing source code. OpenFOAM accomplishes this by combining virtual constructors with the use of simplified base classes as interfaces. As a result, this gives OpenFOAM good extensibility qualities. OpenFOAM refers to this capability as run-time selection.[15]
Structure of OpenFOAM OpenFOAM is constituted by a large base library, which offers the core capabilities of the code:
- Tensor and field operations
- Discretization of partial differential equations using a human-readable syntax
- Solution of linear systems[16]
- Solution of ordinary differential equations[17]
- Automatic parallelization of high-level operations
- Dynamic mesh[18]
- General physical models
- Rheological models[19]
- Thermodynamic models and database[20]
- Turbulence models[21]
- Chemical reaction and kinetics models[22]
- Lagrangian particle tracking methods[23]
- Radiative heat transfer models
- Multi-reference frame and single-reference frame methodologies
- Solvers: they perform the actual calculation to solve a specific continuum mechanics problem.
- Utilities: they are used to prepare the mesh, set-up the simulation case, process the results, and to perform operations other than solving the problem under examination.
Finally, a set of third-party packages are used to provide parallel functionality (OpenMPI) and graphical post-processing (ParaView).
Capabilities
- Basic CFD solvers
- Incompressible flow with RANS and LES capabilities[25]
- Compressible flow solvers with RANS and LES capabilities[26]
- Buoyancy-driven flow solvers[27]
- DNS and LES
- Multiphase flow solvers[28]
- Particle-tracking solvers
- Solvers for combustion problems[29]
- Solvers for conjugate heat transfer[30]
- Molecular dynamics solvers[31]
- Direct simulation Monte Carlo solvers[32]
- Electromagnetics solvers[33]
- Solid dynamics solvers[34]
OpenFOAM utilities are subdivided into:
- Mesh utilities
- Mesh generation: they generate computational grids starting either from an input file (blockMesh), or from a generic geometry specified as STL file, which is meshed automatically with hex-dominant grids (snappyHexMesh)
- Mesh conversion: they convert grids generated using other tools to the OpenFOAM format
- Mesh manipulation: they perform specific operations on the mesh such as localized refinement, definition of regions, and others
- Parallel processing utilities: they provide tools to decompose, reconstruct and re-distribute the computational case to perform parallel calculations
- Pre-processing utilities: tools to prepare the simulation cases
- Post-processing utilities: tools to process the results of simulation cases, including a plugin to interface OpenFOAM and ParaView.
- Surface utilities
- Thermophysical utilities
Advantages and disadvantagesAdvantages
- Friendly syntax for partial differential equations
- Fully documented source code[36]
- Unstructured polyhedral grid capabilities
- Automatic parallelization of applications written using OpenFOAM high-level syntax
- Wide range of applications and models ready to use
- Commercial support and training provided by the developers
- No license costs
- The development community suffers from fragmentation, giving rise to numerous forked projects.
- Absence of an integrated graphical user interface (stand-alone open-source and proprietary options are available)
- The Programmer's guide does not provide sufficient details, making the progress slow if you need to write new applications or add functionality
- FEATool Multiphysics[37] is an easy to use physics simulation toolbox and GUI for MATLAB.
- HELYX-OS[38]
- iconCFD[39]
- InsightCAE[40] is an open source project for creating automated simulation workflows which can be controlled from a GUI ("vertical apps"). OpenFOAM is supported as the primary backend for CFD simulations.
- MantiumFlow[41] - a CLI and GUI tool which automates CFD pre and post-processing, turning simulations into Apps ("vertical apps").
- SimFlow[42]
- SimScale[43]
- simulationHub[44] - online platform with automated cloud based CFD Apps ("vertical apps"), specifically developed for Design engineer
- SwiftBloc[45] and SwiftSnap[46]
- Visual-CFD[47] is an advanced, intelligent environment for OpenFOAM including Pre and Post modules with process Automation/Customization features
- preCICE[48] is an open-source coupling library for partitioned multi-physics simulations.
- ParaView an open-source multiple-platform application for interactive scientific visualization
- "CFD Direct - The Architects of OpenFOAM". CFD Direct. Archived from the original on 27 March 2015.
- "The open source CFD toolbox". OpenFOAM.
- "OpenFOAM Version 1.0". Archived from the original on 7 June 2017.
- "OpenFOAM® History".
- "Release History - OpenFOAM".
- OpenCFD. "OpenFOAM® - Official home of The Open Source Computational Fluid Dynamics (CFD) Toolbox". www.openfoam.com. Archived from the original on 22 September 2016.
- Jasak, Hrvoje (1996). Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows (PDF).
- Chen, Goong; Xiong, Qingang; Morris, Philip J.; Paterson, Eric G.; Sergeev, Alexey Sergeev; Wang, Yi-Ching. (April 2014). "OpenFOAM for Computational Fluid Dynamics". Notices of the American Mathematical Society. 61 (4): 354–363. doi:10.1090/noti1095. ISSN 0002-9920.
- Greenshields, Chris (3 April 2016). "Release History". openfoam.org. Archived from the original on 29 July 2017.
- "Wikki Ltd - About Us".
- "Press Releases: SGI Acquires OpenCFD Ltd., the Leader In Open Source Computational Fluid Dynamics (CFD) Software". SGI. Archived from the original on 6 December 2012. Retrieved 18 December 2012.
- "Acquisition of OpenCFD Ltd., The leader in Open Source software in Computational Fluid Dynamics". ESI Group. 11 September 2012. Archived from the original on 6 December 2012. Retrieved 18 December 2012.
- "OpenFOAM". CFD Direct. 25 March 2015. Archived from the original on 29 March 2015.
- "OpenFOAM Features - CFD Direct". openfoam.org. Archived from the original on 2 April 2015.
- OpenFOAM's run-time selection mechanism explained Archived 8 January 2014 at the Wayback Machine
- "OpenFOAM Features - CFD Direct". openfoam.org. Archived from the original on 2 April 2015.
- "OpenFOAM Features - CFD Direct". openfoam.org. Archived from the original on 2 April 2015.
- "OpenFOAM Features - CFD Direct". openfoam.org. Archived from the original on 27 March 2015.
- "OpenFOAM v5 User Guide: 7.3 Transport/rheology models". cfd.direct. 2 March 2017. Archived from the original on 19 March 2016.
- "OpenFOAM v5 User Guide: 7.1 Thermophysical models". cfd.direct. 2 March 2017. Archived from the original on 19 March 2016.
- "Turbulence Modelling - OpenFOAM - CFD Direct". cfd.direct. Archived from the original on 9 August 2016.
- "OpenFOAM Features - CFD Direct". openfoam.org. Archived from the original on 2 April 2015.
- "OpenFOAM Features - CFD Direct". openfoam.org. Archived from the original on 2 April 2015.
- "OpenFOAM Features - CFD Direct". openfoam.org. Archived from the original on 21 March 2015.
- "OpenFOAM Features - CFD Direct". openfoam.org. Archived from the original on 2 April 2015.
- "OpenFOAM Features - CFD Direct". openfoam.org. Archived from the original on 2 April 2015.
- "OpenFOAM Features - CFD Direct". openfoam.org. Archived from the original on 2 April 2015.
- "Multiphase Flows - OpenFOAM - CFD Direct". cfd.direct. Archived from the original on 9 August 2016.
- "OpenFOAM Features - CFD Direct". openfoam.org. Archived from the original on 2 April 2015.
- "OpenFOAM Features - CFD Direct". openfoam.org. Archived from the original on 2 April 2015.
- "OpenFOAM Features - CFD Direct". openfoam.org. Archived from the original on 2 April 2015.
- "OpenFOAM Features - CFD Direct". openfoam.org. Archived from the original on 2 April 2015.
- "OpenFOAM Features - CFD Direct". openfoam.org. Archived from the original on 2 April 2015.
- "OpenFOAM Features - CFD Direct". openfoam.org. Archived from the original on 2 April 2015.
- Greenshields, Chris (28 April 2016). "Free Software Licence". openfoam.org. Archived from the original on 9 June 2012.
- "OpenFOAM: Free, Open Source Software from the OpenFOAM Foundation". cpp.openfoam.org.
- "FEATool 1.8 with OpenFOAM MATLAB CFD GUI Integration". featool.com. Retrieved 18 May 2018.
- "HELYX-OS GUI for OpenFOAM | ENGYS". engys.com. Retrieved 15 January 2018.
- Administrator. "Setup: iconCFD Process". iconcfd.com. Retrieved 15 January 2018.
- "Open Source Engineering Software - silentdynamics". silentdynamics. Retrieved 7 June 2018.
- "CFD simulation software using OpenFOAM® made as simple as possible". MantiumFlow. Retrieved 27 August 2018.
- "simFlow CFD Software - OpenFOAM® GUI". simFlow CFD. Retrieved 15 January 2018.
- "Open Source Solvers Integrated with SimScale". SimScale. Retrieved 15 January 2018.
- "Components used in simulationHub". Retrieved 7 April 2019.
- "Contrib/SwiftBlock - OpenFOAMWiki". openfoamwiki.net. Retrieved 15 January 2018.
- "Contrib/SwiftSnap - OpenFOAMWiki". openfoamwiki.net. Retrieved 15 January 2018.
- "Visual-CFD for OpenFOAM®". openfoam.com. Retrieved 5 May 2018.
- "preCICE". Retrieved 24 March 2019.
Turbulence modeling
Ansys- Turbulence modeling
------------------------------------------------------------------------------------------------------------------------
Turbulence modelling
----------------------------------------------------------------------------------------------------------------------
(Source: https://en.wikipedia.org/wiki/Turbulence_modeling)
Turbulence modeling is the construction and use of a mathematical model to predict the effects of turbulence. Turbulent flows are commonplace in most real life scenarios, including the flow of blood through the cardiovascular system[1], the airflow over an aircraft wing[2], the re-entry of space vehicles[3], besides others. In spite of decades of research, there is no analytical theory to predict the evolution of these turbulent flows. The equations governing turbulent flows can only be solved directly for simple cases of flow. For most real life turbulent flows, CFD simulations use turbulent models to predict the evolution of turbulence. These turbulence models are simplified constitutive equations that predict the statistical evolution of turbulent flows[4].
 from the convective acceleration. This term is known as the Reynolds stress,
from the convective acceleration. This term is known as the Reynolds stress,  .[5] Its effect on the mean flow is like that of a stress term, such as from pressure or viscosity.
.[5] Its effect on the mean flow is like that of a stress term, such as from pressure or viscosity.
To obtain equations containing only the mean velocity and pressure, we need to close the RANS equations by modelling the Reynolds stress term as a function of the mean flow, removing any reference to the fluctuating part of the velocity. This is the closure problem.
as a function of the mean flow, removing any reference to the fluctuating part of the velocity. This is the closure problem.
 , the turbulence eddy viscosity, has been introduced. Models of this type are known as eddy viscosity models or EVM's.
, the turbulence eddy viscosity, has been introduced. Models of this type are known as eddy viscosity models or EVM's.
More general turbulence models have evolved over time, with most modern turbulence models given by field equations similar to the Navier–Stokes equations.
 . The S–A model uses only one additional equation to model turbulence viscosity transport, while the k–ε and k–ω models use two.
. The S–A model uses only one additional equation to model turbulence viscosity transport, while the k–ε and k–ω models use two.
Sallam,
Ahmed; Hwang, Ned (1984). "Human red blood cell hemolysis in a
turbulent shear flow: contribution of Reynolds shear stresses". Biorheology.
Rhie, C; Chow, Li (1983). "Numerical study of the turbulent flow past an airfoil with trailing edge separation". AIAA Journal.
Reddy, K; Silva, D; Krishnendu, Sinha (1983). "Hypersonic turbulent flow simulation of Fire II reentry vehicle afterbody". AIAA Journal.
Pope, Stephen (2000). Turbulent Flows.
Andersson, Bengt; et al. (2012). Computational fluid dynamics for engineers. Cambridge: Cambridge University Press. p. 83. ISBN 978-1-107-01895-2.
Boussinesq, Joseph (1903). Boussinesq,
J. (1903). Thōrie analytique de la chaleur mise en harmonie avec la
thermodynamique et avec la thōrie mc̄anique de la lumi_re:
Refroidissement et c̄hauffement par rayonnement, conductibilit ̄des
tiges, lames et masses cristallines, courants de convection, thōrie
mc̄anique de la lumi_re. Gauthier-Villars.
John J. Bertin; Jacques Periaux; Josef Ballmann, Advances in Hypersonics: Modeling hypersonic flows
Prandtl, Ludwig (1925). "Bericht uber Untersuchungen zur ausgebildeten Turbulenz". Zs. angew. Math. Mech. 2.
Smagorinsky,
Joseph (1963). "Smagorinsky, Joseph. "General circulation experiments
with the primitive equations: I. The basic experiment". Monthly Weather Review. 91 (3).
Spalart, P.; Allmaras, S. (1992). "A one-equation turbulence model for aerodynamic flows". 30th aerospace sciences meeting and exhibit, AIAA.
Hanjalic, K.; Launder, B. (1972). "A Reynolds stress model of turbulence and its application to thin shear flows". Journal of Fluid Mechanics.
Wilcox, D. C. (2008). "Formulation of the k-omega Turbulence Model Revisited". AIAA Journal.
Menter, F. R. (1994). "Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications". AIAA Journal.
Hanjalić, Hanjalić; Launder, Brian (2011). Modelling Turbulence in Engineering and the Environment: Second-Moment Routes to Closure.
Mishra,
Aashwin; Girimaji, Sharath (2013). "Intercomponent energy transfer in
incompressible homogeneous turbulence: multi-point physics and
amenability to one-point closures". Journal of Fluid Mechanics. 731: 639–681. Bibcode:2013JFM...731..639M. doi:10.1017/jfm.2013.343.
Pope, Stephen. "Turbulent Flows". Cambridge University Press, 2000.
Lumley, John; Newman, Gary (1977). "The return to isotropy of homogeneous turbulence". Journal of Fluid Mechanics. 82: 161–178. Bibcode:1977JFM....82..161L. doi:10.1017/s0022112077000585.
Mishra,
Aashwin; Girimaji, Sharath (2013). "Intercomponent energy transfer in
incompressible homogeneous turbulence: multi-point physics and
amenability to one-point closures". Journal of Fluid Mechanics. 731: 639–681. Bibcode:2013JFM...731..639M. doi:10.1017/jfm.2013.343.
-------------------------------------------------------------------------------------------------------------------------
(Source: https://www.cfd-online.com/Wiki/Turbulence_modeling)
------------------------------------------------------------------------------------------------------------------------
Turbulence modelling
(Source: https://en.wikipedia.org/wiki/Turbulence_modeling)
Turbulence modeling is the construction and use of a mathematical model to predict the effects of turbulence. Turbulent flows are commonplace in most real life scenarios, including the flow of blood through the cardiovascular system[1], the airflow over an aircraft wing[2], the re-entry of space vehicles[3], besides others. In spite of decades of research, there is no analytical theory to predict the evolution of these turbulent flows. The equations governing turbulent flows can only be solved directly for simple cases of flow. For most real life turbulent flows, CFD simulations use turbulent models to predict the evolution of turbulence. These turbulence models are simplified constitutive equations that predict the statistical evolution of turbulent flows[4].
Contents
Closure problem
The Navier–Stokes equations govern the velocity and pressure of a fluid flow. In a turbulent flow, each of these quantities may be decomposed into a mean part and a fluctuating part. Averaging the equations gives the Reynolds-averaged Navier–Stokes (RANS) equations, which govern the mean flow. However, the nonlinearity of the Navier–Stokes equations means that the velocity fluctuations still appear in the RANS equations, in the nonlinear term from the convective acceleration. This term is known as the Reynolds stress,
from the convective acceleration. This term is known as the Reynolds stress,  .[5] Its effect on the mean flow is like that of a stress term, such as from pressure or viscosity.
.[5] Its effect on the mean flow is like that of a stress term, such as from pressure or viscosity.
To obtain equations containing only the mean velocity and pressure, we need to close the RANS equations by modelling the Reynolds stress term
 as a function of the mean flow, removing any reference to the fluctuating part of the velocity. This is the closure problem.
as a function of the mean flow, removing any reference to the fluctuating part of the velocity. This is the closure problem.
Eddy viscosity
Joseph Valentin Boussinesq was the first to attack the closure problem[6], by introducing the concept of eddy viscosity. In 1877 Boussinesq proposed relating the turbulence stresses to the mean flow to close the system of equations. Here the Boussinesq hypothesis is applied to model the Reynolds stress term. Note that a new proportionality constant , the turbulence eddy viscosity, has been introduced. Models of this type are known as eddy viscosity models or EVM's.
, the turbulence eddy viscosity, has been introduced. Models of this type are known as eddy viscosity models or EVM's.
- Which can be written in shorthand as
- where
is the mean rate of strain tensor
is the turbulence eddy viscosity
is the turbulence kinetic energy
- and
is the Kronecker delta.
Prandtl's mixing-length concept
Later, Ludwig Prandtl introduced the additional concept of the mixing length[8], along with the idea of a boundary layer. For wall-bounded turbulent flows, the eddy viscosity must vary with distance from the wall, hence the addition of the concept of a 'mixing length'. In the simplest wall-bounded flow model, the eddy viscosity is given by the equation:- where:
is the partial derivative of the streamwise velocity (u) with respect to the wall normal direction (y);
is the mixing length.
More general turbulence models have evolved over time, with most modern turbulence models given by field equations similar to the Navier–Stokes equations.
Smagorinsky model for the sub-grid scale eddy viscosity
Joseph Smagorinsky was the first who proposed a formula for the eddy viscosity in Large Eddy Simulation models[9], based on the local derivatives of the velocity field and the local grid size:Spalart–Allmaras, k–ε and k–ω models
The Boussinesq hypothesis is employed in the Spalart–Allmaras (S–A), k–ε (k–epsilon), and k–ω (k–omega) models and offers a relatively low cost computation for the turbulence viscosity . The S–A model uses only one additional equation to model turbulence viscosity transport, while the k–ε and k–ω models use two.
. The S–A model uses only one additional equation to model turbulence viscosity transport, while the k–ε and k–ω models use two.
Common models
The following is a brief overview of commonly employed models in modern engineering applications.
The Spalart–Allmaras model[10]
is a one-equation model that solves a modelled transport equation for
the kinematic eddy turbulent viscosity. The Spalart–Allmaras model was
designed specifically for aerospace applications involving wall-bounded
flows and has been shown to give good results for boundary layers
subjected to adverse pressure gradients. It is also gaining popularity
in turbomachinery applications.[citation needed]
K-epsilon (k-ε) turbulence model[11]is the most common model used in computational fluid dynamics (CFD) to simulate mean flow characteristics for turbulent flow conditions. It is a two-equation model which gives a general description of turbulence by means of two transport equations (PDEs). The original impetus for the K-epsilon model was to improve the mixing-length model, as well as to find an alternative to algebraically prescribing turbulent length scales in moderate to high complexity flows.
In computational fluid dynamics, the k–omega (k–ω) turbulence model[12] is a common two-equation turbulence model that is used as a closure for the Reynolds-averaged Navier–Stokes equations (RANS equations). The model attempts to predict turbulence by two partial differential equations for two variables, k and ω, with the first variable being the turbulence kinetic energy (k) while the second (ω) is the specific rate of dissipation (of the turbulence kinetic energy k into internal thermal energy).
SST (Menter's shear stress transport) turbulence model[13] is a widely used and robust two-equation eddy-viscosity turbulence model used in computational fluid dynamics. The model combines the k-omega turbulence model and K-epsilon turbulence model such that the k-omega is used in the inner region of the boundary layer and switches to the k-epsilon in the free shear flow.
The Reynolds stress equation model (RSM), also referred to as second moment closure model[14], is the most complete classical turbulence modelling approach. Popular eddy-viscosity based models like the k–ε (k–epsilon) model and the k–ω (k–omega) models have significant shortcomings in complex engineering flows. This arises due to the use of the eddy-viscosity hypothesis in their formulation. For instance, in flows with high degrees of anisotropy, significant streamline curvature, flow separation, zones of recirculating flow or flows influenced by rotational effects, the performance of such models is unsatisfactory.[15] In such flows, Reynolds stress equation models offer much better accuracy.[16]
Eddy viscosity based closures cannot account for the return to isotropy of turbulence,[17] observed in decaying turbulent flows. Eddy-viscosity based models cannot replicate the behaviour of turbulent flows in the Rapid Distortion limit,[18] where the turbulent flow essentially behaves like an elastic medium[19].
K-epsilon (k-ε) turbulence model[11]is the most common model used in computational fluid dynamics (CFD) to simulate mean flow characteristics for turbulent flow conditions. It is a two-equation model which gives a general description of turbulence by means of two transport equations (PDEs). The original impetus for the K-epsilon model was to improve the mixing-length model, as well as to find an alternative to algebraically prescribing turbulent length scales in moderate to high complexity flows.
In computational fluid dynamics, the k–omega (k–ω) turbulence model[12] is a common two-equation turbulence model that is used as a closure for the Reynolds-averaged Navier–Stokes equations (RANS equations). The model attempts to predict turbulence by two partial differential equations for two variables, k and ω, with the first variable being the turbulence kinetic energy (k) while the second (ω) is the specific rate of dissipation (of the turbulence kinetic energy k into internal thermal energy).
SST (Menter's shear stress transport) turbulence model[13] is a widely used and robust two-equation eddy-viscosity turbulence model used in computational fluid dynamics. The model combines the k-omega turbulence model and K-epsilon turbulence model such that the k-omega is used in the inner region of the boundary layer and switches to the k-epsilon in the free shear flow.
The Reynolds stress equation model (RSM), also referred to as second moment closure model[14], is the most complete classical turbulence modelling approach. Popular eddy-viscosity based models like the k–ε (k–epsilon) model and the k–ω (k–omega) models have significant shortcomings in complex engineering flows. This arises due to the use of the eddy-viscosity hypothesis in their formulation. For instance, in flows with high degrees of anisotropy, significant streamline curvature, flow separation, zones of recirculating flow or flows influenced by rotational effects, the performance of such models is unsatisfactory.[15] In such flows, Reynolds stress equation models offer much better accuracy.[16]
Eddy viscosity based closures cannot account for the return to isotropy of turbulence,[17] observed in decaying turbulent flows. Eddy-viscosity based models cannot replicate the behaviour of turbulent flows in the Rapid Distortion limit,[18] where the turbulent flow essentially behaves like an elastic medium[19].
References
Notes
- Sagaut, Pierre; Cambon, Claude (2008). Homogeneous Turbulence Dynamics.
Other
- Townsend, A.A. (1980) "The Structure of Turbulent Shear Flow" 2nd Edition (Cambridge Monographs on Mechanics), ISBN 0521298199
- Bradshaw, P. (1971) "An introduction to turbulence and its measurement" (Pergamon Press), ISBN 0080166210
- Wilcox C. D., (1998), "Turbulence Modeling for CFD" 2nd Ed., (DCW Industries, La Cañada), ISBN 0963605100
(Source: https://www.cfd-online.com/Wiki/Turbulence_modeling)
Turbulence modeling is a key issue in most CFD simulations. Virtually all engineering applications are turbulent and hence require a turbulence model.
Classes of turbulence models
- RANS-based models
- Linear eddy-viscosity models
- Algebraic models
- One and two equation models
- Non-linear eddy viscosity models and algebraic stress models
- Reynolds stress transport models
- Linear eddy-viscosity models
- Large eddy simulations
- Detached eddy simulations and other hybrid models
- Direct numerical simulations
Content of turbulence modeling section
- Turbulence
- RANS-based turbulence models
- Large eddy simulation (LES)
- Detached eddy simulation (DES)
- Direct numerical simulation (DNS)
- Turbulence near-wall modeling
- Turbulence free-stream boundary conditions
Đăng ký:
Nhận xét (Atom)








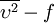 model
model
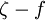 model
model