Ansys- Turbulence modeling
------------------------------------------------------------------------------------------------------------------------
Turbulence modelling
----------------------------------------------------------------------------------------------------------------------
(Source:
https://en.wikipedia.org/wiki/Turbulence_modeling)
Turbulence modeling is the construction and use of a
mathematical model to predict the effects of
turbulence. Turbulent flows are commonplace in most real life scenarios, including the flow of blood through the cardiovascular system
[1], the airflow over an aircraft wing
[2], the re-entry of space vehicles
[3],
besides others. In spite of decades of research, there is no analytical
theory to predict the evolution of these turbulent flows. The equations
governing turbulent flows can only be solved directly for simple cases
of flow. For most real life turbulent flows,
CFD simulations
use turbulent models to predict the evolution of turbulence. These
turbulence models are simplified constitutive equations that predict the
statistical evolution of turbulent flows
[4].
Closure problem
The
Navier–Stokes equations
govern the velocity and pressure of a fluid flow. In a turbulent flow,
each of these quantities may be decomposed into a mean part and a
fluctuating part. Averaging the equations gives the
Reynolds-averaged Navier–Stokes (RANS) equations,
which govern the mean flow. However, the nonlinearity of the
Navier–Stokes equations means that the velocity fluctuations still
appear in the RANS equations, in the nonlinear term

from the convective acceleration. This term is known as the
Reynolds stress,

.
[5] Its effect on the mean flow is like that of a stress term, such as from pressure or viscosity.
To obtain equations containing only the mean velocity and
pressure, we need to close the RANS equations by modelling the Reynolds
stress term

as a function of the mean flow, removing any reference to the fluctuating part of the velocity. This is the
closure problem.
Eddy viscosity
Joseph Valentin Boussinesq was the first to attack the closure problem
[6], by introducing the concept of
eddy viscosity.
In 1877 Boussinesq proposed relating the turbulence stresses to the
mean flow to close the system of equations. Here the Boussinesq
hypothesis is applied to model the Reynolds stress term. Note that a new
proportionality constant

, the turbulence eddy viscosity, has been introduced. Models of this type are known as eddy viscosity models or EVM's.

- Which can be written in shorthand as

- where
 is the mean rate of strain tensor
is the mean rate of strain tensor  is the turbulence eddy viscosity
is the turbulence eddy viscosity is the turbulence kinetic energy
is the turbulence kinetic energy- and
 is the Kronecker delta.
is the Kronecker delta.
In this model, the additional turbulence stresses are given by augmenting the
molecular viscosity with an eddy viscosity.
[7] This can be a simple constant eddy viscosity (which works well for some free
shear flows such as axisymmetric jets, 2-D jets, and mixing layers).
Prandtl's mixing-length concept
Later,
Ludwig Prandtl introduced the additional concept of the mixing length
[8], along with the idea of a
boundary layer.
For wall-bounded turbulent flows, the eddy viscosity must vary with
distance from the wall, hence the addition of the concept of a 'mixing
length'. In the simplest wall-bounded flow model, the eddy viscosity is
given by the equation:

- where:
 is the partial derivative of the streamwise velocity (u) with respect to the wall normal direction (y);
is the partial derivative of the streamwise velocity (u) with respect to the wall normal direction (y);
 is the mixing length.
is the mixing length.
This simple model is the basis for the "
law of the wall", which is a surprisingly accurate model for wall-bounded, attached (not separated) flow fields with small
pressure gradients.
More general
turbulence models have evolved over time, with most modern turbulence models given by
field equations similar to the
Navier–Stokes equations.
Smagorinsky model for the sub-grid scale eddy viscosity
Joseph Smagorinsky was the first who proposed a formula for the eddy viscosity in Large Eddy Simulation models
[9], based on the local derivatives of the velocity field and the local grid size:

In the context of
Large Eddy Simulation,
turbulence modeling refers to the need to parameterize the subgrid
scale stress in terms of features of the filtered velocity field. This
field is called
subgrid-scale modeling.
Spalart–Allmaras, k–ε and k–ω models
The Boussinesq hypothesis is employed in the
Spalart–Allmaras (S–A),
k–ε (
k–epsilon), and
k–ω (
k–omega) models and offers a relatively low cost computation for the turbulence viscosity

. The S–A model uses only one additional equation to model turbulence viscosity transport, while the
k–ε and
k–ω models use two.
Common models
The following is a brief overview of commonly employed models in modern engineering applications.
The Spalart–Allmaras model
[10]
is a one-equation model that solves a modelled transport equation for
the kinematic eddy turbulent viscosity. The Spalart–Allmaras model was
designed specifically for aerospace applications involving wall-bounded
flows and has been shown to give good results for boundary layers
subjected to adverse pressure gradients. It is also gaining popularity
in turbomachinery applications.
[citation needed]
K-epsilon (k-ε) turbulence model
[11]is
the most common model used in computational fluid dynamics (CFD) to
simulate mean flow characteristics for turbulent flow conditions. It is a
two-equation model which gives a general description of turbulence by
means of two transport equations (PDEs). The original impetus for the
K-epsilon model was to improve the mixing-length model, as well as to
find an alternative to algebraically prescribing turbulent length scales
in moderate to high complexity flows.
In computational fluid dynamics, the k–omega (k–ω) turbulence model
[12]
is a common two-equation turbulence model that is used as a closure for
the Reynolds-averaged Navier–Stokes equations (RANS equations). The
model attempts to predict turbulence by two partial differential
equations for two variables, k and ω, with the first variable being the
turbulence kinetic energy (k) while the second (ω) is the specific rate
of dissipation (of the turbulence kinetic energy k into internal thermal
energy).
SST (Menter's shear stress transport) turbulence model
[13]
is a widely used and robust two-equation eddy-viscosity turbulence
model used in computational fluid dynamics. The model combines the
k-omega turbulence model and K-epsilon turbulence model such that the
k-omega is used in the inner region of the boundary layer and switches
to the k-epsilon in the free shear flow.
The Reynolds stress equation model (RSM), also referred to as second moment closure model
[14], is the most complete classical turbulence modelling approach. Popular eddy-viscosity based models like the
k–ε (k–epsilon) model and the
k–ω (k–omega)
models have significant shortcomings in complex engineering flows. This
arises due to the use of the eddy-viscosity hypothesis in their
formulation. For instance, in flows with high degrees of anisotropy,
significant streamline curvature, flow separation, zones of
recirculating flow or flows influenced by rotational effects, the
performance of such models is unsatisfactory.
[15] In such flows, Reynolds stress equation models offer much better accuracy.
[16]
Eddy viscosity based closures cannot account for the return to isotropy of turbulence,
[17]
observed in decaying turbulent flows. Eddy-viscosity based models
cannot replicate the behaviour of turbulent flows in the Rapid
Distortion limit,
[18] where the turbulent flow essentially behaves like an elastic medium
[19].
References
Notes
Sallam,
Ahmed; Hwang, Ned (1984). "Human red blood cell hemolysis in a
turbulent shear flow: contribution of Reynolds shear stresses". Biorheology.
Rhie, C; Chow, Li (1983). "Numerical study of the turbulent flow past an airfoil with trailing edge separation". AIAA Journal.
Reddy, K; Silva, D; Krishnendu, Sinha (1983). "Hypersonic turbulent flow simulation of Fire II reentry vehicle afterbody". AIAA Journal.
Pope, Stephen (2000). Turbulent Flows.
Andersson, Bengt; et al. (2012). Computational fluid dynamics for engineers. Cambridge: Cambridge University Press. p. 83. ISBN 978-1-107-01895-2.
Boussinesq, Joseph (1903). Boussinesq,
J. (1903). Thōrie analytique de la chaleur mise en harmonie avec la
thermodynamique et avec la thōrie mc̄anique de la lumi_re:
Refroidissement et c̄hauffement par rayonnement, conductibilit ̄des
tiges, lames et masses cristallines, courants de convection, thōrie
mc̄anique de la lumi_re. Gauthier-Villars.
John J. Bertin; Jacques Periaux; Josef Ballmann, Advances in Hypersonics: Modeling hypersonic flows
Prandtl, Ludwig (1925). "Bericht uber Untersuchungen zur ausgebildeten Turbulenz". Zs. angew. Math. Mech. 2.
Smagorinsky,
Joseph (1963). "Smagorinsky, Joseph. "General circulation experiments
with the primitive equations: I. The basic experiment". Monthly Weather Review. 91 (3).
Spalart, P.; Allmaras, S. (1992). "A one-equation turbulence model for aerodynamic flows". 30th aerospace sciences meeting and exhibit, AIAA.
Hanjalic, K.; Launder, B. (1972). "A Reynolds stress model of turbulence and its application to thin shear flows". Journal of Fluid Mechanics.
Wilcox, D. C. (2008). "Formulation of the k-omega Turbulence Model Revisited". AIAA Journal.
Menter, F. R. (1994). "Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications". AIAA Journal.
Hanjalić, Hanjalić; Launder, Brian (2011). Modelling Turbulence in Engineering and the Environment: Second-Moment Routes to Closure.
Mishra,
Aashwin; Girimaji, Sharath (2013). "Intercomponent energy transfer in
incompressible homogeneous turbulence: multi-point physics and
amenability to one-point closures". Journal of Fluid Mechanics. 731: 639–681. Bibcode:2013JFM...731..639M. doi:10.1017/jfm.2013.343.
Pope, Stephen. "Turbulent Flows". Cambridge University Press, 2000.
Lumley, John; Newman, Gary (1977). "The return to isotropy of homogeneous turbulence". Journal of Fluid Mechanics. 82: 161–178. Bibcode:1977JFM....82..161L. doi:10.1017/s0022112077000585.
Mishra,
Aashwin; Girimaji, Sharath (2013). "Intercomponent energy transfer in
incompressible homogeneous turbulence: multi-point physics and
amenability to one-point closures". Journal of Fluid Mechanics. 731: 639–681. Bibcode:2013JFM...731..639M. doi:10.1017/jfm.2013.343.
- Sagaut, Pierre; Cambon, Claude (2008). Homogeneous Turbulence Dynamics.
Other
- Townsend, A.A. (1980) "The Structure of Turbulent Shear Flow" 2nd Edition (Cambridge Monographs on Mechanics), ISBN 0521298199
- Bradshaw, P. (1971) "An introduction to turbulence and its measurement" (Pergamon Press), ISBN 0080166210
- Wilcox C. D., (1998), "Turbulence Modeling for CFD" 2nd Ed., (DCW Industries, La Cañada), ISBN 0963605100
-------------------------------------------------------------------------------------------------------------------------
(Source:
https://www.cfd-online.com/Wiki/Turbulence_modeling)
Turbulence modeling is a key issue in most CFD simulations. Virtually
all engineering applications are turbulent and hence require a
turbulence model.
Classes of turbulence models
- RANS-based models
- Linear eddy-viscosity models
- Algebraic models
- One and two equation models
- Non-linear eddy viscosity models and algebraic stress models
- Reynolds stress transport models
- Detached eddy simulations and other hybrid models
- Direct numerical simulations
Content of turbulence modeling section
- Turbulence
- RANS-based turbulence models
- Linear eddy viscosity models
- Algebraic models
- Cebeci-Smith model
- Baldwin-Lomax model
- Johnson-King model
- A roughness-dependent model
- One equation models
- Prandtl's one-equation model
- Baldwin-Barth model
- Spalart-Allmaras model
- Rahman-Siikonen-Agarwal Model
- Two equation models
- k-epsilon models
- Standard k-epsilon model
- Realisable k-epsilon model
- RNG k-epsilon model
- Near-wall treatment
- k-omega models
- Wilcox's k-omega model
- Wilcox's modified k-omega model
- SST k-omega model
- Near-wall treatment
- Realisability issues
- Kato-Launder modification
- Durbin's realizability constraint
- Yap correction
- Realisability and Schwarz' inequality
- Nonlinear eddy viscosity models
- Explicit nonlinear constitutive relation
- Cubic k-epsilon
- Explicit algebraic Reynolds stress models (EARSM)
- v2-f models
-
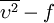 model
model
-
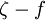 model
model
- Reynolds stress model (RSM)
- Large eddy simulation (LES)
- Smagorinsky-Lilly model
- Dynamic subgrid-scale model
- RNG-LES model
- Wall-adapting local eddy-viscosity (WALE) model
- Kinetic energy subgrid-scale model
- Near-wall treatment for LES models
- Structural modeling
- Detached eddy simulation (DES)
- Direct numerical simulation (DNS)
- Turbulence near-wall modeling
- Turbulence free-stream boundary conditions
- Turbulence intensity
- Turbulence length scale

















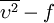 model
model
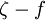 model
model